[toc]
算法基础
基础概念特征
1.定义
算法(Algorithm)是一个有穷规则(或语句、指令)的有序集合。它确定了解决某一问题的一个运算序列。对于问题的初始输入,通过算法有限步的运行,产生一个或多个输出。
数据的逻辑结构与存储结构密切相关:
- 算法设计: 取决于选定的逻辑结构
- 算法实现: 依赖于采用的存储结构
2.算法的特性
- 有穷性 —— 算法执行的步骤(或规则)是有限的;
- 确定性 —— 每个计算步骤无二义性;
- 可行性 —— 每个计算步骤能够在有限的时间内完成;
- 输入 ,输出 —— 存在数据的输入和出输出
3.评价算法好坏的方法
- 正确性:运行正确是一个算法的前提。
- 可读性:容易理解、容易编程和调试、容易维护。
- 健壮性:考虑情况全面,不容以出现运行错误。
- 时间效率高:算法消耗的时间少。
- 储存量低:占用较少的存储空间。
时间复杂度
算法效率——用依据该算法编制的程序在计算机上执行所消耗的时间来度量。“O”表示一个数量级的概念。根据算法中语句执行的最大次数(频度)来 估算一个算法执行时间的数量级。
计算方法:
写出程序中所有运算语句执行的次数,进行加和
如果得到的结果是常量则时间复杂度为1
如果得到的结果中存在变量n则取n的最高次幂作为时间复杂度
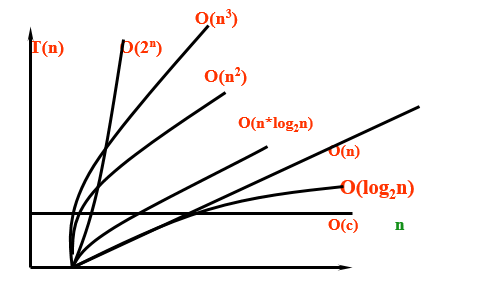
下图表示随问题规模n的增大,算法执行时间的增长率。

排序和查找
排序
排序(Sort)是将无序的记录序列(或称文件)调整成有序的序列。
常见排序方法:
先初始化排序方法类:
class Sort:
def __init__(self, list_):
self.list_ = list_
冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
def bubble(self):
# 外层循环表示比较多少轮
for i in range(len(self.list_) - 1):
# 内层循环表示每轮比较的次数
for j in range(len(self.list_) - i - 1):
# 前一个数比后一个数大则交换位置
if self.list_[j] > self.list_[j + 1]:
self.list_[j], self.list_[j + 1] = \
self.list_[j + 1], self.list_[j]
选择排序

工作原理为,首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。以此类推,直到所有元素均排序完毕。
def select(self):
# 比较多少轮
for i in range(len(self.list_) - 1):
min = i # 假定i号位置数字最小
for j in range(i + 1, len(self.list_)):
if self.list_[min] > self.list_[j]:
min = j
if i != min:
self.list_[i], self.list_[min] = \
self.list_[min], self.list_[i]
插入排序

对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
def insert(self):
for i in range(1, len(self.list_)):
x = self.list_[i]
j = i
while j > 0 and self.list_[j - 1] > x:
self.list_[j] = self.list_[j - 1]
j -= 1
self.list_[j] = x
快速排序

从数列中挑出一个元素,称为 “基准”(pivot),
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
这里需要使用到递归的思想
# 一轮交换
def sub_sort(self, low, high):
key = self.list_[low] # 基准数字
while low < high:
# 后面的数向前甩
while low < high and self.list_[high] >= key:
high -= 1
self.list_[low] = self.list_[high]
# 前面的数向后甩
while low < high and self.list_[low] < key:
low += 1
self.list_[high] = self.list_[low]
self.list_[low] = key
return low
# 快排函数
def quick(self, low, high):
# low 列表开头元素索引
# high 列表结尾元素索引
if low < high:
key = self.sub_sort(low, high)
self.quick(low, key - 1)
self.quick(key + 1, high)