阶跃函数
$f(x) = \begin{cases}0, x \leq 0 \cr 1, x > 0 \end{cases}$
函数图像

sigmoid函数
$y=\frac{1}{1+e_{}^{-x}}$
函数图像

由于阶跃函数的输出结果具有跳跃性,且只有0和1这2个输出结果,所以导致了他在向量机中可以表现良好,但是在神经网络的训练中的效果并没有sigmoid函数的效果好。
sigmoid函数相较于阶跃函数具有连续性,这样就可以输出连续的新号值,而不是0或1这2个单独的信号值!
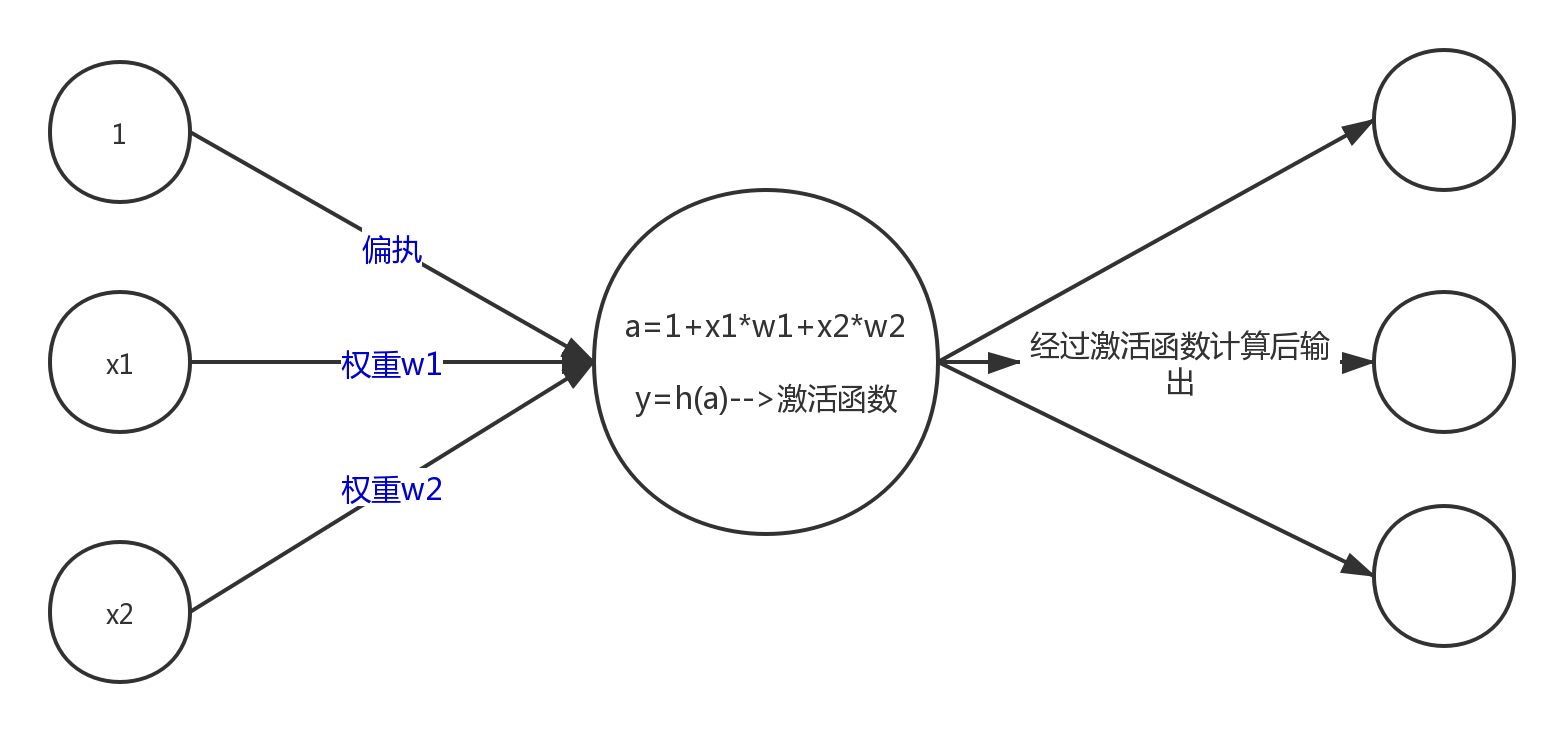
激活函数图解