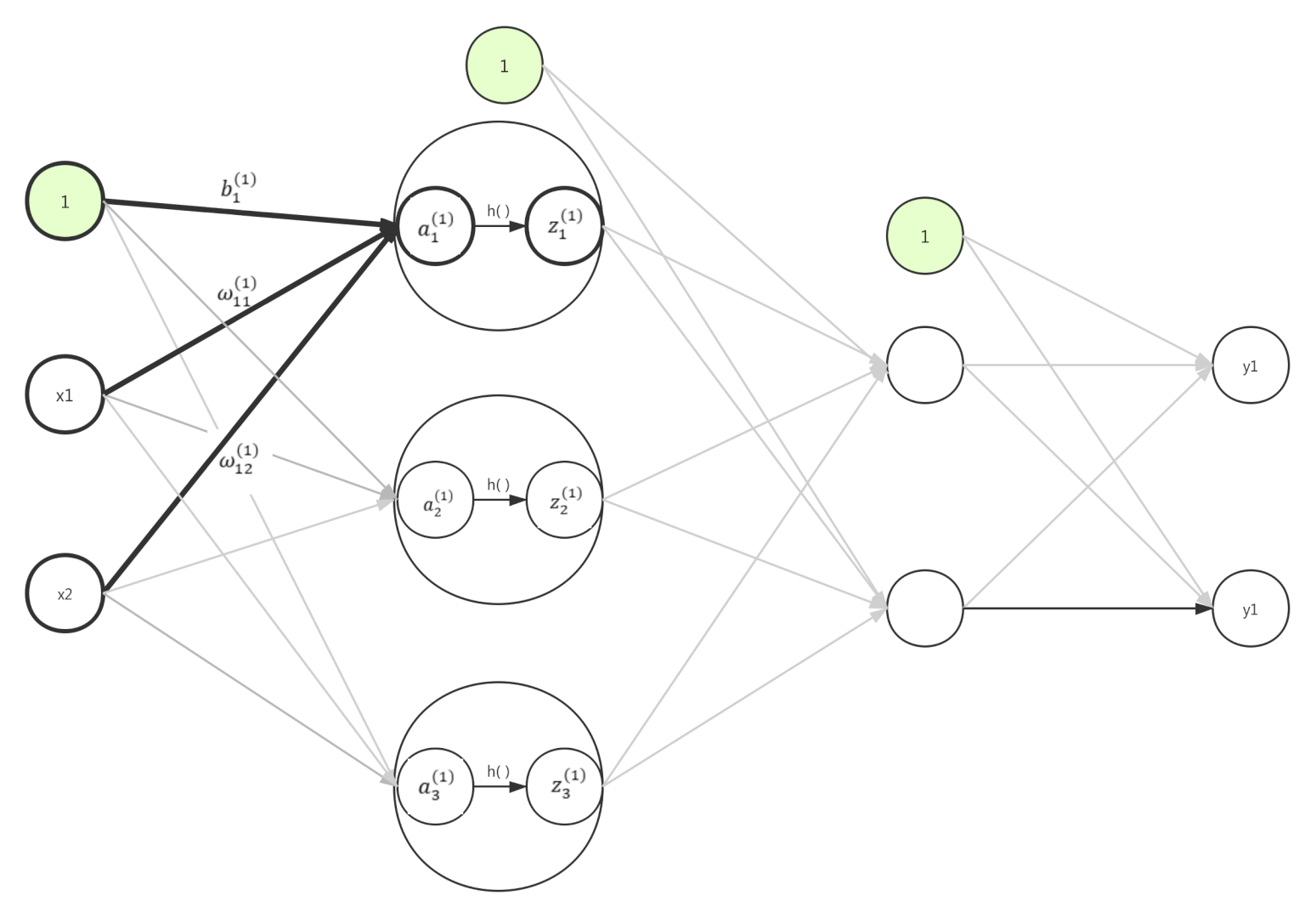
从输入层到第一层信号传递视图

其中$h()$函数就是sigmoid函数，即：$z_{1}=sigmoid(a_{1})$

第一层到第二层与第二层到输出层的参数传递类似，但是输出层的激活函数不在使用$sigmoid$ 改为使用恒等函数输出

恒等函数

即输入什么数值，返回什么数值！

def identity_function(x):
    return x

代码实现

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    
    return network

def forward(network, x):    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']    
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1    
    z1 = sigmoid(a1)    
    a2 = np.dot(z1, W2) + b2    
    z2 = sigmoid(a2)    
    a3 = np.dot(z2, W3) + b3    
    y = identity_function(a3)
    return y

定义了2个方法，其中init_network()是用来初始化各层的参数，权重、偏执之类的。

forward就是干脆直接的接受参数与输入，然后算出结果。这2个函数就组成了一个简单的3层神经网络

其中forward()函数中的sigmoid()函数为激活函数

见文章“从跃迁函数到激活函数”

其中forward（前向）单词，表示从输入方向开始，一直计算到输出方向。在神经网络的训练中，还有后向（backward）的计算方式。